World's Best AI Learning Platform with profoundly Demanding Certification Programs
Designed by IITians, only for AI Learners.
Download our e-book of Introduction To Python
Related Blog
Top Discussion
+256704300651- Psychic lost love Spell Caster // Divorce Spell // Marriage Proposal +256704300651 == WASHINGTON DC// TOP DEATH SPELLS @POWERFUL REVENGE DEATH SPELL CASTER IN USA,CANADA, UK, CALIFONIA, MEXICO, IRELAND, NY, CANADA, LONDON, SWEDEN, BOTSWANA Exception Type: JSONDecodeError at /update/ Exception Value: Expecting value: line 1 column 1 (char 0) How can I write Python code to change a date string from "mm/dd/yy hh: mm" format to "YYYY-MM-DD HH: mm" format? ((+256704300651}} INSTANT DEATH SPELL CASTER / REVENGE SPELL/ VOODOO A SPELL CASTER/╬ ₩௹]+256704300651₩௹]╬MAMA ZAMIE A TRADITIONAL HEALER /SANGOMA AND A SPIRITUAL HEALER in BELGIUM, +256704300651.. === Revenge Death spells caster In Denmark / Sweden / Germany / spell caster, revenge spell, spell caster review, witchcraft, psychic, magic forum. ↩⁜↪ +91-9352799565↩⁜↪ Divorce Problem Solution IN mumbai Join Discussion
Top Courses
Master's In Artificial Intelligence Job Guarantee Program
4.5 (1,292 Ratings)
559 Learners
Webinars
Why You Should Learn Data Science in 2023?
Jun 8th (7:00 PM) 289 Registered
Loss Functions in Deep Learning
Sanober Ibrahim
a year ago
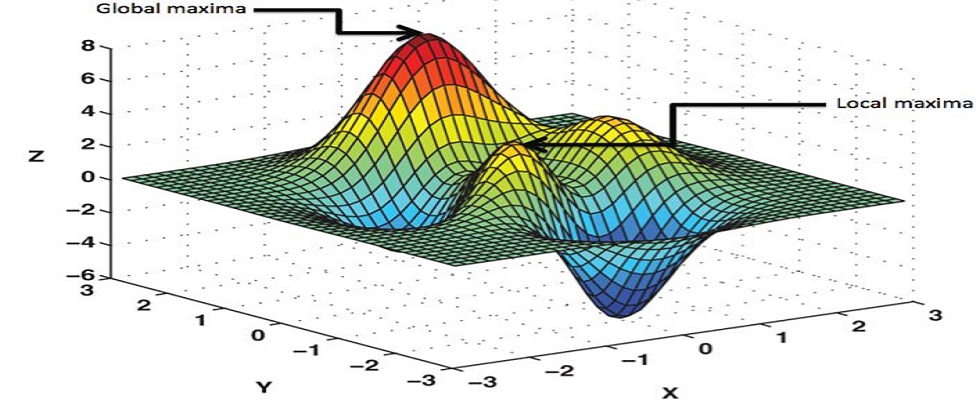
Table of Contents
- What Is a Loss Function?
- Types of Loss Functions
1. Regression Loss Functions
2. Binary Classification Loss Functions
3. Multi-class Classification Loss Functions
- Regression Loss Functions
1. Squared Error Loss
L1 and L2 loss
2. Huber Loss
3. Pseudo-Huber loss function
- Binary Classification Loss Functions
1. Hinge Loss
2. Cross-entropy loss
3. Sigmoid-Cross-entropy loss
4. Softmax cross-entropy loss
All of us
may already familiar with the process involved to train a deep learning neural network.
But let me remind you in a brief.
We train deep learning neural
networks using the gradient descent optimization algorithm which provides the
idea of how and in which direction we can move to achieve minimum error so that
the deep learning model performs the best.
In this optimization algorithm,
the error for the current state of the model is estimated repeatedly. Now it requires
to choose which error function (loss function) that can be used
to calculate the loss of the model so that the weights can be updated and the
loss can be reduced for the next evaluation process.
Now you may have the basic idea
about how a deep neural network gets trained. Let’s move further and try to
understand it in a better way.
What Is a Loss Function?
In a simplest way, we can say that a
loss function is a method of evaluating how well your algorithm models your
dataset.
In terms of optimization techniques,
the function which is used to evaluate a solution is referred to as the objective
function. Now we may want to maximize or minimize the objective function so
to get the highest or lowest score respectively.
Typically, for deep
learning neural network, we want to minimize the error value and hence the
objective function here is known as a cost function or a loss
function and the value of this objection function is simply referred as the
“loss”.
NOTE: Is there any difference between a Loss Function and a Cost Function?
I
want to clear you this here – although the cost
function and the loss function are
synonymous and used interchangeably but they are a little bit different actually.
When
we have a single training example then it is known as loss function. It is also
sometimes called as an error function. On the other hand, a cost
function is the average loss over the entire training dataset.
Now that we are familiar with what is loss function and loss,
we need to know what functions to use when and why?
Types of loss functions
There are mainly three types of loss functions we have and again
these loss functions are further divided which is shown as below
1. Regression Loss Functions
- Mean Squared Error Loss
- Mean Squared Logarithmic Error Loss
- Mean Absolute Error Loss
- L1 Loss
- L2 Loss
- Huber Loss
- Pseudo Huber Loss
2. Binary Classification Loss Functions
- Binary Cross-Entropy
- Hinge Loss
- Squared Hinge Loss
3. Multi-class Classification Loss Functions
- Multi-class Cross Entropy Loss
- Sparse Multiclass Cross-Entropy Loss
- Kullback Leibler Divergence Loss
Regression Loss Functions
As of
now, you must be quite familiar with linear regression problems. Linear
Regression problem deals with mapping a linear relationship between a dependent
variable, Y,
and several independent
variables, X’s.
So, we essentially fit a line in space on these variables to get the best model
with minimum error. Basically, a regression problem involves predicting a
real-valued quantity.
In this
article I will try to take you through some of the loss functions and later I
will try to write separate article on each of the different loss functions.
1. Squared Error Loss
L1 and L2 loss
L1 and L2 are two common loss functions in machine
learning/deep learning which are mainly used to minimize the error.
L1 loss function is also known as Least Absolute Deviations in short LAD. L2 loss function is
also known as Least square errors in
short LS.
Let's get brief idea about these two loss functions
L1 Loss function
It is used to minimize the error which is the sum of all the
absolute differences in between the true value and the predicted value.
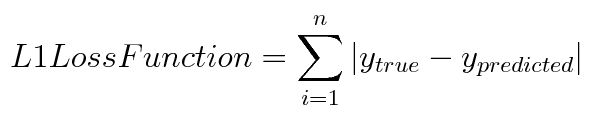
L1 loss is also known as the Absolute Error and the cost is the Mean of these Absolute Errors (MAE).
L2 Loss Function
It is also used to minimize the error which is the sum of all the
squared differences in between the true value and the predicted value.
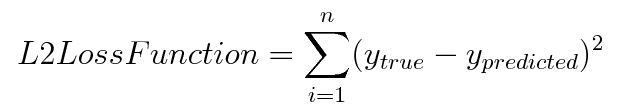
The corresponding cost function is the Mean of these Squared
Errors (MSE).
Note: The
disadvantage of
the L2 norm is that when
there are outliers, these points will account for the main component of the
loss.
For
example, the true value is 1, the prediction is 10 times, the prediction value
is 1000 once, and the prediction value of the other times is about 1, obviously
the loss value is mainly dominated by 1000.
Plotting
L1 and L2 loss using TensorFlow
#import libraries
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
x_pre = tf.lin_space(-1., 1., 100)
x_actual = tf.constant(0,dtype=tf.float32)
l1_loss = tf.abs((x_pre - x_actual))
l2_loss = tf.square((x_pre - x_actual))
with tf.Session() as sess:
x_,l1_,l2_ = sess.run([x_pre, l1_loss, l2_loss])
plt.plot(x_,l1_,label='l1_loss')
plt.plot(x_,l2_,label='l2_loss')
plt.legend()
plt.show()
Output: The above code will produce below plot:
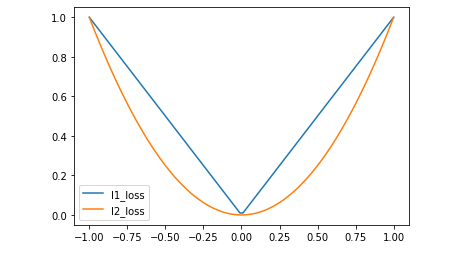
2. Huber Loss
Huber
Loss is often used in regression problems. Compared with L2 loss, Huber Loss is
less sensitive to outliers (because if the residual is too large, it is a
piecewise function, loss is a linear function of the residual).
The Huber loss combines the best properties of MSE and MAE.
It is quadratic for smaller errors and is linear otherwise (and similarly for
its gradient). It is identified by its delta parameter
Among them, 𝛿 is a set parameter, 𝑦 represents the real
value and f(x) represent the predicted value.
The advantage of this is
that when the residual is small, the loss function is L2 norm, and when the
residual is large, it is a linear function of L1 norm.
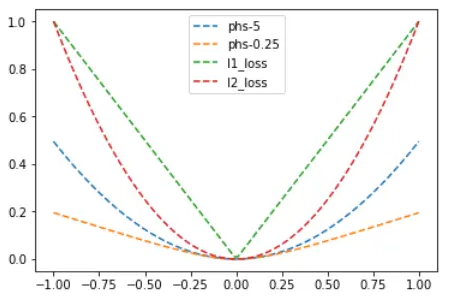
3. Pseudo-Huber loss function
A smooth approximation of Huber loss to ensure that each order is
differentiable.
Where δ is the set parameter, the larger the value, the steeper the linear part on both sides. You can observe it with the help of plot given below.
Binary Classification Loss Functions
Binary Classification is
simply classifying an object into one of two classes. This classification is
based on a rule applied to the input feature vector. For example, classifying that
today rain will happen or not happen, say its subject line, this is binary
classification problem. Let’s see some of the loss functions associated with
it.
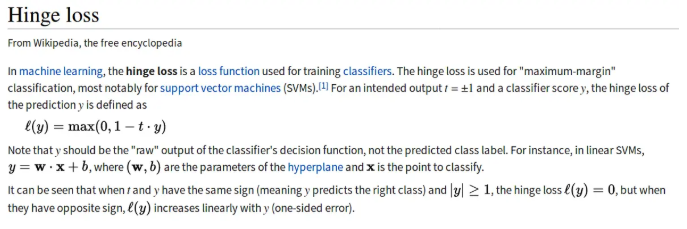
1. Hinge Loss
Hinge loss is often used for binary classification problems, such
as ground true: t = 1 or -1, predicted value
y = wx + b
In the svm classifier, the definition of hinge loss is:
In other
words, the closer the y is to t, the smaller the loss will be.
2. Cross-entropy loss
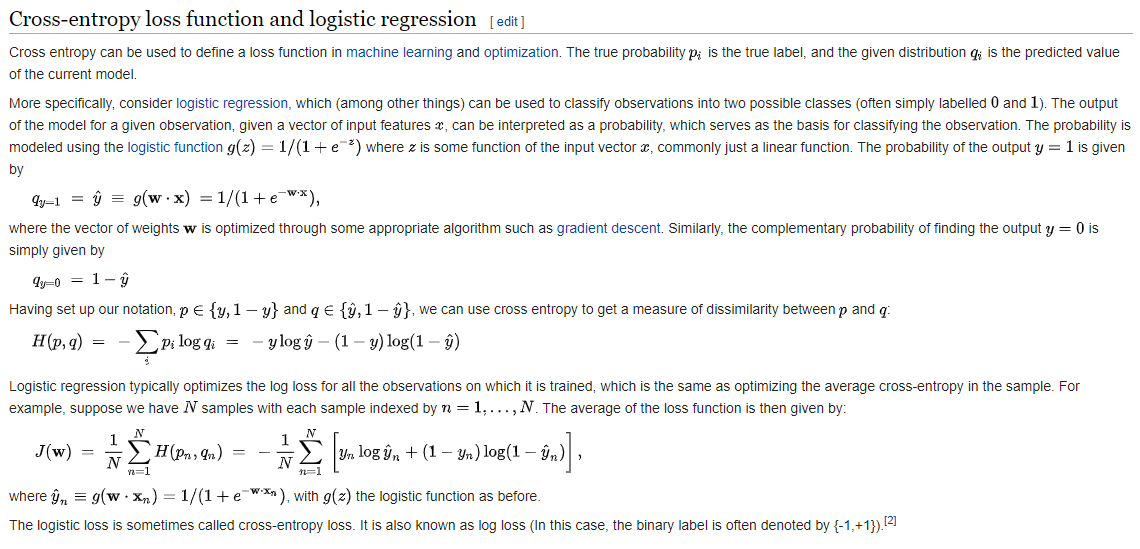
The above
is mainly to say that cross-entropy loss is mainly applied to binary
classification problems. The predicted value is a probability value and the
loss is defined according to the cross-entropy. Note the value range of the
above value: the predicted value of y should be a probability and the value
range are [0,1].
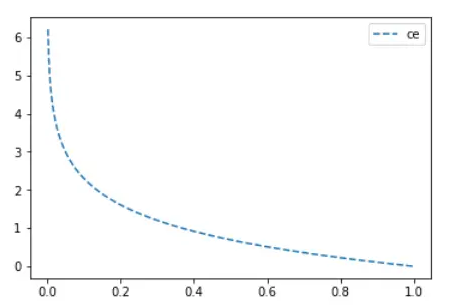
3. Sigmoid-Cross-entropy loss
The above
cross-entropy loss requires that the predicted value is a probability.
Generally, we calculate scores=x * w+b. Entering this value into the sigmoid function can compress
the value range to (0,1).
It can be
seen that the sigmoid function smooths the predicted value(such as directly
inputting 0.1 and 0.01 and inputting 0.1, 0.01 sigmoid and then entering, the
latter will obviously have a much smaller change value), which makes the predicted value of sigmoid-ce far from the label loss growth is not so steep.
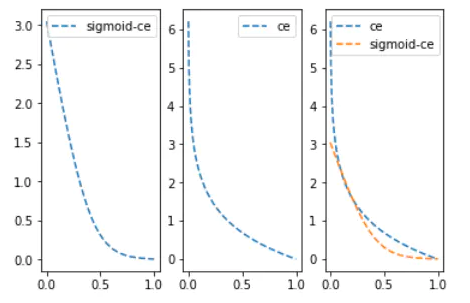
4. Softmax cross-entropy loss
First, the softmax function
can convert a set of fraction vectors into corresponding probability vectors.
Here is the definition of softmax function.
As above, softmax also
implements a vector of 'squashes' k-dimensional real value to the [0,1] range
of k-dimensional, while ensuring that the cumulative sum is 1.
According to the
definition of cross entropy, probability is required as input. Sigmoid cross entropy
loss uses sigmoid to convert the score vector into a probability vector, and
softmax-cross-entropy-loss uses a softmax function to convert the score vector
into a probability vector.
According to the
definition of cross-entropy loss.
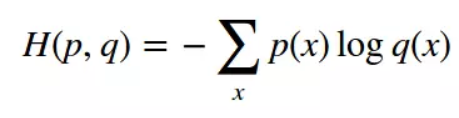
As above, softmax also
implements a vector of 'squashes' k-dimensional real value to the [0,1] range
of k-dimensional, while ensuring that the cumulative sum is 1.
According to the
definition of cross entropy, probability is required as input. Sigmoid cross entropy
loss uses sigmoid to convert the score vector into a probability vector, and
softmax-cross-entropy-loss uses a softmax function to convert the score vector
into a probability vector.
According to the
definition of cross entropy loss.
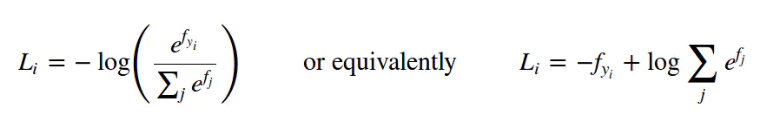
Where fj is the score of all possible categories,
and fyi is the
score of ground true class.
I hope you enjoyed reading this article and finally, you came
to know about Loss Functions in Deep Learning.
For more such blogs/courses on data science, machine
learning, artificial intelligence and emerging new technologies do visit us at InsideAIML.
Thanks for reading…
Happy Learning…