
Download our e-book of Introduction To Python
Related Blog
Matplotlib - Subplot2grid() FunctionDiscuss Microsoft Cognitive ToolkitMatplotlib - Working with ImagesMatplotlib - PyLab moduleMatplotlib - Working With TextMatplotlib - Setting Ticks and Tick LabelsCNTK - Creating First Neural NetworkMatplotlib - MultiplotsMatplotlib - Quiver PlotPython - Chunks and Chinks View More
Top Discussion
How can I write Python code to change a date string from "mm/dd/yy hh: mm" format to "YYYY-MM-DD HH: mm" format? Which sorting technique is used by sort() and sorted() functions of python? How to use Enum in python? Can you please help me with this error? I was just selecting some random columns from the diabetes dataset of sklearn. Decision tree is a classification algo...How can it be applied to load diabetes dataset which has DV continuous Objects in Python are mutable or immutable? How can unclassified data in a dataset be effectively managed when utilizing a decision tree-based classification model in Python? How to leave/exit/deactivate a Python virtualenvironment Join Discussion
Top Courses
Webinars
Decision Tree in Python

Chiranjivi Viru
2 years ago
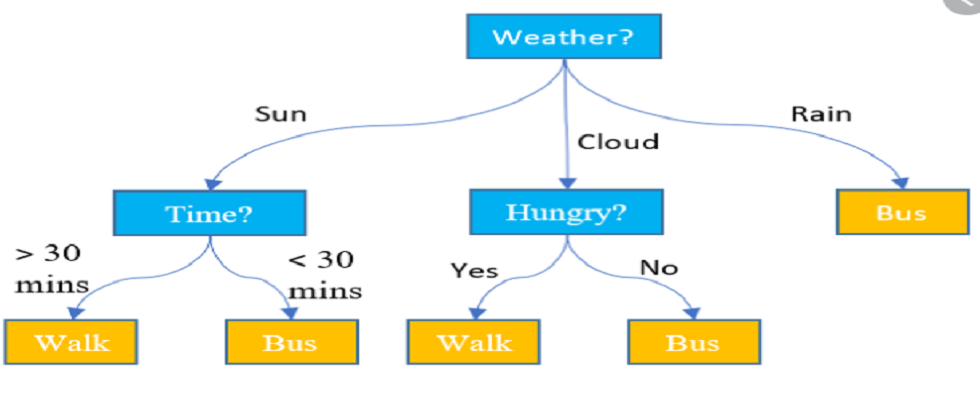
Table of Contents
- Introduction.
- Types of Decision Trees.
1. Categorical Decision Tree
2. Continues Decision Tree
- Terminology related to Decision Tree
- How decision tree works?
- Entropy
- Information Gain
Introduction
Classification or Regression can be categorized in two steps that is learning and predicting. In the first stage learning, the algorithm will learn from the training data and predict the unseen data in the second stage that is prediction. For these prediction part we are having plenty of algorithms, in all these algorithms Decision tree algorithm has its own value and demand in these set of algorithms because of its high interpret-ability and systematic representation.
Decision tree comes under the family of supervised learning algorithms. unlike other algorithms decision tree has capability to handle classification and regression based problems.
The goal of decision tree helps to find the value or class of the target variable from the algorithm which has learned by the prior data or training data.
Types of Decision Trees
In general Decision tree has two types:
Categorical Decision Tree
If a target variable contains categorical column, which includes binary levels or multi level uses categorical Decision Tree.
Continues Decision Tree
If a target variable contains continues values(might be in decimals) uses continues Decision tree.
Let me take a example and explain you clearly:-
Example
If they are handling a problem like loan payments. Customer will be paying his loan amount or not. That is here we are trying to predict (yes/no). This comes under problem of Categorical Decision Tree. In second stage we have to predict, how much amount will be payed to bank, as here the target variable is continues it comes for Continues Decision tree.
Terminology related to Decision Tree
1. Root Node:- Root Node gives us the information that particular attribute is more important in the Data Set. So, our algorithm selected that feature or attribute as a root node. This root node is selected based on entropy or Information gain.
2. Splitting:- The process of splitting node into two or more sub-nodes.
3. Decision Node:- When sub-node splits into another sub-node, then is called Decision Node, because here splitting is based on decision of the sub-node.
4. Leaf or Terminal Node:- Nodes which can't be further split is known as Leaf Node or Terminal Node.
5. Pruning:- When we cut or trim the sub-nodes of a decision node, this process is called Pruning, In simple words we can say pruning is the opposite of splitting.
6. Branch or Sub-tree:- The sub-section or sub part of entire tree is know as Branch.
6. Parent Node & Child Node:- A node which can which can be split is known as Parent Node and these sub-nodes are known as Child Nodes.
How decision tree works?
The decision of making strategic splits affects on the accuracy of the model. The decision criteria is different for classification and regression.
It uses entropy or Information gain to select the root node and from there the splitting starts. For the next split it selects the node which has low entropy or high Information gain. Entropy helps in identifying the randomness of the model. While coming to pruning part as Machine Learning expert we should decide the pruning part. That is up-to which part of the tree have to pruned. If we prune too much model will be affected with under fitting or If we allowed to make more splits, model will be suffered with over fitting.
Entropy
Entropy is the measure of randomness. If we are having the higher entropy, it is difficult to draw conclusions out of that information. So, that always we should select entropy that is having less value.
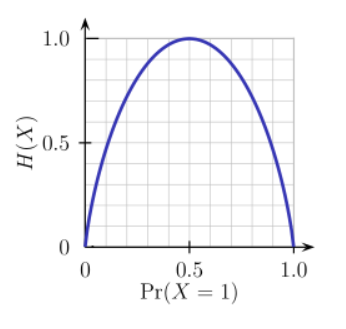
From the above graph, we can clearly say that H(X), the entropy is zero when the probability value is 0 or 1. We can find the maximum entropy when the probability value is 0.5. That is the reason why, we can't make any conclusion, when we have high entropy.
Information Gain
In simple terminology we can say Information gain is (Entropy before split) - (Entropy after split). Information Gain, or IG for short, measures the reduction in entropy or surprise by splitting a dataset according to a given value of a random variable.
A larger information gain suggests a lower entropy group or groups of samples, and hence less surprise.
Enjoyed reading this blog? Then why not share it with others. Help us make this AI community stronger.
To learn more about such concepts related to Artificial Intelligence, visit our insideAIML blog page.
You can also ask direct queries related to Artificial Intelligence, Deep Learning, Data Science and Machine Learning on our live insideAIML discussion forum.
Keep Learning. Keep Growing.
