Adam Optimizer: In-depth explanation

Neha Kumawat

4 years ago

In my previous article “Optimizers in Machine Learning and Deep Learning.” I gave a brief introduction about Adam optimizers. In this article, I will try to give an in-depth explanation of the optimizer’s algorithm.

If you didn’t read my previous articles. I recommend you to first go through my previous articles on optimizers mentioned below and then come back to this article for more better understanding:

Optimizers in Machine Learning and Deep Learning

Gradient descent Algorithm: In-Depth explanation

Adagrad and Adadelta optimizers

RMSprop: In-depth Explanation

So, let’s start

Adam stands for Adaptive Moment Estimation, is another method that computes adaptive learning rates for each parameter. In addition to storing an exponentially decaying average of past squared gradients like Adadelta and RMSprop.

Adam also keeps an exponentially decaying average of past gradients, similar to momentum.

Adam can be viewed as a combination of Adagrad and RMSprop, (Adagrad) which works well on sparse gradients and (RMSProp) which works well in online and nonstationary settings respectively.

Adam implements the exponential moving average of the gradients to scale the learning rate instead of a simple average as in Adagrad. It keeps an exponentially decaying average of past gradients.

Adam is computationally efficient and has very less memory requirement.

Adam optimizer is one of the most popular and famous gradient descent optimization algorithms.

Intuition behind Adam

We can simply say that, do everything that RMSProp does to solve the denominator decay problem of AdaGrad. In addition to that, use a cumulative history of gradients that how Adam optimizers work.

The updating rule for Adam is shown below

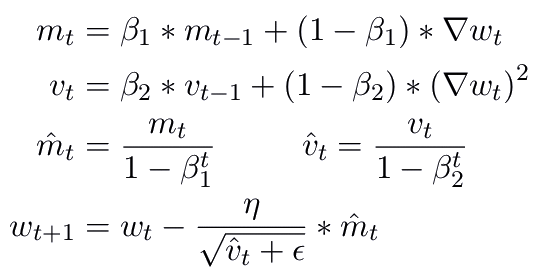
If you have already gone through my previous article on optimizers and especially RMSprop optimizer then you may notice that the update rule for Adam optimizer is much similar to RMSProp optimizer, except notations and help we also look at the cumulative history of gradients (m_t).

Note that the third step in the update rule above is used for bias correction.

RMSProp implementation in Python

So, we can define Adam function in python as shown below.

def adam():

w, b, eta, max_epochs = 1, 1, 0.01, 100, 
mw, mb, vw, vb, eps, beta1, beta2 = 0, 0, 0, 0, 1e-8, 0.9, 0.99

for i in range(max_epochs):
          dw, db = 0, 0
          for x,y in data:
                     dw+= grad_w(w, b, x, y)
                     db+= grad_b(w, b, x, y)
          mw = beta1 * mw + (1-beta1) * dw
          mb = beta1 * mb + (1-beta1) * db
          vw = beta2 * vw + (1-beta2) * dw**2
          vb = beta2 * vb + (1-beta2) * db**2
          mw = mw/(1-beta1**(i+1))
          mb = mb/(1-beta1**(i+1))                     
          vw = vw/(1-beta2**(i+1))
          vb = vb/(1-beta2**(i+1))
          w = w - eta * mw/np.sqrt(vw + eps)
          b = b - eta * mb/np.sqrt(vb + eps)
   print(error(w,b))

Below given is a step by step working of Adam optimizer.

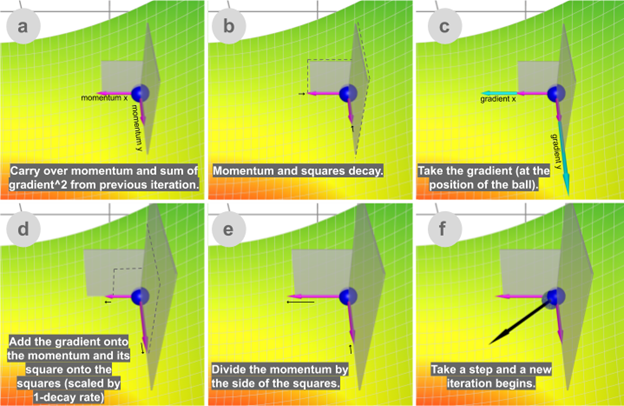
Steps involved are:

a) Carry over momentum and sum of gradient square from the previous iteration.

b) Take momentum and square decay.

c) Then, take gradient at the position of the ball as shown in the figure above.

d) Next, add the gradient onto the momentum and its square onto square (scaled by 1-decay)

e) Then divide the momentum by the side of the square.

f) Finally, take a step and a new iteration begins as shown in the figure.

Note: if you want to watch live animation I recommend you to visit this app.

It will provide you a very good visualization.

Note: We can say that Adam gets the speed from momentum and the ability to adapt gradients in different directions from RMSProp. The combination of these two makes it powerful and faster among all the other optimizers.

I hope after reading this article, finally, you came to know about what is Adam, how it works? and What’s the difference between Adam and other optimizers algorithms and You also see how it is most important optimizer. In the next articles, I will come with a detailed explanation of some other type of optimizers. For more blogs/courses on data science, machine learning, artificial intelligence and new technologies do visit us at InsideAIML.

Thanks for reading…

Related Blog

Top Discussion

Top Courses

Webinars

Adam Optimizer: In-depth explanation

Intuition behind Adam

RMSProp implementation in Python

Submit Review